Séance TD-3 : Echantilonnage#
Exercice 1 :#
Effet de l’échantillonnage
Soit le signal suivant : \(x(t)=\cos(2 \pi f_0 t), \; f_0=10\) kHz.
Tracer la transformée de Fourier de \(x(t)\): \(X(f)\).
Solution
La transformée de Fourier de \(x(t)\), \(X(f)\), est tracée sur la figure suivante.

Est-il possible d’échantillonner \(x(t)\) sans perte d’information ? Si oui à quelle condition ?
Solution
Il est possible d’échantillonner \(x(t)\) sans perte d’information en utilisant une fréquence d’échantillonnage
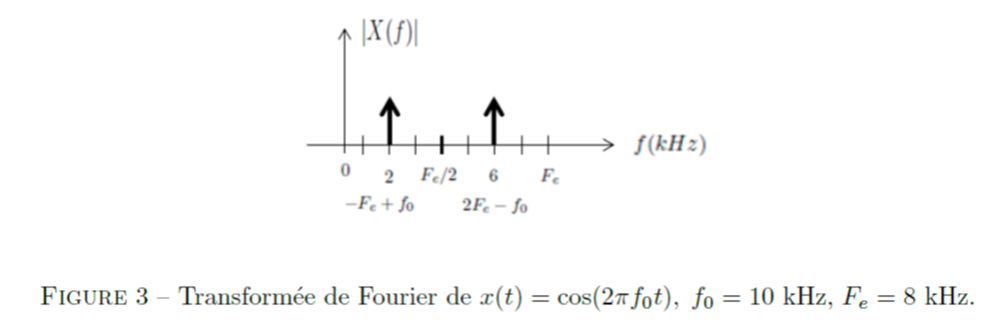
\[F_e>2f_0=20 \text{ kHz (respect de la condition de Shannon)}\]Tracer, entre \(0\) et \(F_e\), la transformée de Fourier de \(x(t)\) échantillonné à \(T_e=1/F_e\) quand :
a. \(F_e=30\) kHz.
b. \(F_e=8\) kHz.
Solution
La transformée de Fourier de \(x(t)\), échantillonné à \(T_e=1/F_e\), est tracée entre \(0\) et \(F_e\) sur les figures suivantes quand \(F_e=30\) kHz et quand \(F_e=8\) kHz.

A partir des échantillons nous souhaitons reconstruire \(x(t)\) par filtrage passe-bas à \(F_e/2\). Quels seront les signaux obtenus pour chaque fréquence d’échantillonnage précédente ?
Solution
Par filtrage passe-bas à \(F_e/2\), nous obtenons
\[x(t)=\cos(2 \pi f_0 t), \text{ avec} f_0=10 \text{ kHz pour } F_e=30 \text{ kHz}\]\[x(t)=\cos(2 \pi f_1 t), \text{ avec} f_1=2 \text{ kHz pour } F_e=8 \text{ kHz}\]
Exercice 2 :#
Echantillonneur moyenneur
L’échantillonneur moyenneur est une méthode pratique d’échantillonnage qui consiste à calculer, toutes les \(T_e\) secondes (période d’échantillonnage), la valeur moyenne du signal pendant un intervalle de temps \(\theta \) (\(\theta <<T_e\)) et à affecter cette valeur moyenne à l’échantillon discrétisé :
Démontrer que le signal échantillonné \(x_{ech}(t)\) peut se mettre sous la forme :
\[ x_{ech}(t)=\frac{1}{\theta }\left[ \Pi _{\theta }\left( t\right) \ast x\left( t-\frac{\theta }{2}\right) \right] .\amalg \hspace{-0.3cm}\amalg_{T_e}\left( t\right) \]où \(\Pi _{\theta }\left( t\right) \) et \(\amalg \hspace{-0.3cm}\amalg_{T_e}\left( t\right) \) représentent respectivement la fenêtre rectangulaire de largeur \(\theta\) et le peigne de Dirac de période \(T_e\).
Solution
\[x_{ech}(t)=\sum_k y\left( kT_e\right) \delta \left( t-kT_e\right)= y(t) \sum_k \delta \left( t-kT_e\right)=y(t) .\amalg \hspace{-0.3cm}\amalg_{T_e}\left( t\right)\]Reste à montrer que
\[y(t)=\frac{1}{\theta }\left[ \Pi _{\theta }\left( t\right) \ast x\left( t-\frac{\theta }{2}\right) \right],\]que l’on obtient de la manière suivante
\[\begin{align*} y(t)&=\frac{1}{\theta }\int_{t-\theta }^{t}x(u)du\\ &=\frac{1}{\theta}\int_{-\infty }^{+\infty}x(u) \times \Pi_{\theta}\left(u-\left(t-\frac{\theta}{2}\right)\right) du\\ &=\frac{1}{\theta}\int_{-\infty }^{+\infty}x(u) \times \Pi_{\theta}\left(\left(t-\frac{\theta}{2}\right)-u\right) du\\ &=\frac{1}{\theta }\left(x \ast \Pi_{\theta}\right)\left(t-\frac{\theta}{2}\right) \end{align*}\]En déduire la transformée de Fourier correspondante \(X_{ech}\left( f\right) \).
Solution
\[\begin{align*} X_{ech}(f)&= Y(f) \ast \frac{1}{T_e} \amalg \hspace{-0.3cm}\amalg_{1/T_e}\left( f\right)\\ &=\frac{1}{T_e}\sum_k Y\left( f-\frac{k}{T_e}\right), \text{ avec } Y(f)=sinc(\pi f \theta) X(f) e^{-j \pi f \theta} \end{align*}\]En considérant un signal à support spectral borné \(2\Delta f\) et en prenant en compte que la fonction \(sinc(\pi \theta f)\) peut être supposée constante sur l’intervalle \(\left[ -\frac{1}{3\theta },\frac{1}{3\theta }\right] \)
\[ sinc(\pi \theta f)=\frac{\sin (\pi \theta f)}{\pi \theta f}\approx 1 \; \text{pour }f\in \left[ -\frac{1}{3\theta },\frac{1}{3\theta }\right] \]a. quelle(s) condition(s) doit vérifier \(\theta \) pour que le signal \(x(t)\) puisse être restitué par filtrage de \(x_{ech}(t)\) ?
Solution
Il faut que \(\Delta f \leq \frac{1}{3\theta} \Leftrightarrow \theta \leq \frac{1}{3\Delta f}\)
b. Dans ces conditions peut-on échantillonner à la fréquence de Shannon ?
Solution
Après filtrage antialiasing on pourra prendre \(F_e\) tel que \(\Delta f < \frac{F_e}{2}=\frac{1}{2T_e} \Leftrightarrow T_e< \frac{1}{2\Delta f}\)
Exercice 3 :#
Echantillonnage d’un signal à spectre non borné
Soit le signal \(x(t)\) défini par :
Déterminer la transformée de Fourier \(X(f)\) du signal \(x(t)\). Tracer \(\left|X(f)\right|\).
Solution
\[X(f)=\int_{0}^{+\infty} e^{-(a+j 2 \pi f)t} dt=\frac{1}{a+j 2 \pi f}\]\[\left|X(f)\right|=\frac{1}{\sqrt{a^2+ 4 \pi^2 f^2}}\]Le signal \(x(t)\) est-il échantillonnable sans perte d’information ? Expliquez votre réponse.
Solution
Non car le spectre n’est pas borné. Il n’est donc pas possible d’appliquer la condition de Shannon.
En considérant la transformée de Fourier comme négligeable pour une atténuation minimale de \(40\) dB par rapport à sa valeur maximum, dimensionner la fréquence d’échantillonnage, \(F_e\), à utiliser.
Solution
On a le maximum du spectre pour \(f=0\). On souhaite donc trouver \(F_{max}\) telle que :
\[10 \log_{10}\left|X(F_{max})\right|^2 \leq 10 \log_{10}\left|X(0)\right|^2-10 \log_{10}\left(10^4\right)=10 \log_{10} \frac{\left|X(0)\right|^2}{10^4}\]D’où
\[\frac{1}{\sqrt{a^2+ 4 \pi^2 F_{max}^2}}\leq \frac{1}{10^4 a^2}\]et donc
\[F_{max}^2\geq \frac{\left(10^4-1\right) a^2}{4 \pi^2}\]Soit, en négligeant \(1\) devant \(10^4\) :
\[F_{max}\geq \frac{100 a}{2 \pi} \text{ et donc } F_e\geq \frac{100 a}{\pi}\]Une fois \(F_e\) déterminée, quel traitement doit-on appliquer au signal avant de l’échantillonner ?
Solution
Un filtre anti repliement afin de tronquer le spectre du signal à \(F_{max}\).
