Un exemple: le code (5,7)_8
Contents
3.1. Un exemple: le code \((5,7)_8\)#
3.1.1. Représentation et notations#
La représentation sous forme de registre à décalage du code convolutif \((5,7)_8\) est donnée par la figure XXX.
C’est un code qui a un bit d’information \(u[n]\) en entrée fait correspondre deux sorties \(c_1[n]\) et \(c_2[n]\) comme données sur la figure Fig. 3.1.
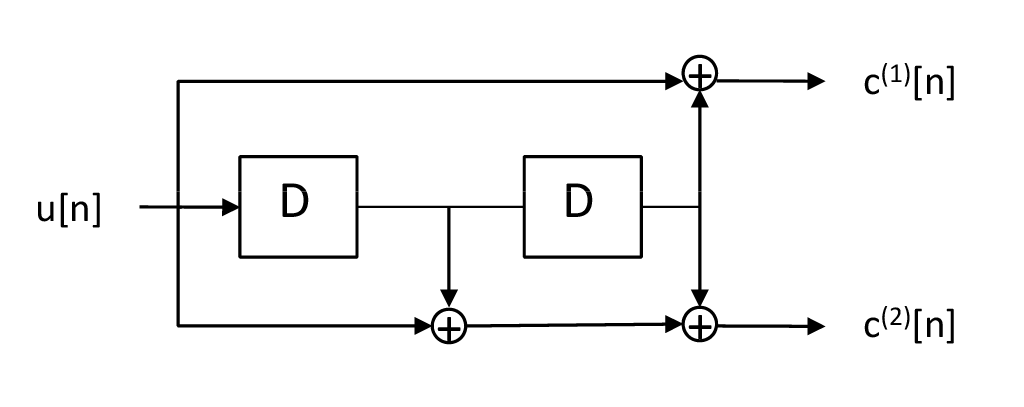
Fig. 3.1 Code convolutif \((5,7)\)#
Les positions du registre qui permettent de calculer les sorties codées par \(\mathrm{OU}\)-exclusif (addition sur GF(2)/addition mod-\(2\)) peuvent être représentées par des vecteurs \(g^{(1)}=[1 0 1]= [5]_8\) et \(g^{(2)}=[ 1 1 1]=[7]_8\). Si on note \(D\) l’opérateur du retard, on peut également rencontrer la représentation polynômiale suivante \(g^{(1)}(D)=1 + D^2\) et \(g^{(2)}(D)=1 + D + D^2\). Le rendement de codage est défini par \(R=k/n=1/2\) (\(k\) entrées, \(n\) sorties). La mémoire \(\nu\) du code est définie comme le nombre de bits dans le registre et la longueur de contrainte est donnée par \(l_c=\nu+1\).
3.1.2. Relations entrées-sorties#
Soit \(u[n]\) la séquence d’entrée, on a alors comme sorties
où \(\circledast\) représente le produit de convolution sur \(GF(2)\) (d’où le nom de code convolutif).
On introduit généralement la transformée en \(D\) telle
Cette transformée est l’équivalent de la transformée en \(\mathcal{Z}\) où l’opérateur \(D\) est préféré à l’opérateur \(z^{-1}\) pour la définition de l’opérateur du retard. Ainsi toute convolution se traduit dans le domaine associé par le produit des polynômes, ie.
On peut alors adopter la notation polynomiale suivante \(c^{(i)}(D)=u(D) g^{(i)}(D), \; \forall i \in \{1,2\}\). On obtient au final la Représentation vectorielle polynomiale
où \(G(D)\) matrice génératrice polynômiale de taille \(k \times n\).
3.1.3. Terminaison de codage#
Pour un code convolutif, différents types de terminaison pour le codage sont possibles.
Troncature directe :
Dans cette méthode, le codage s’arrête quand on n’a plus de bits d’information à coder. Dans ce cadre, le codeur peut terminer dans n’importe quel état de sa mémoire (le contenu du registre est alors quelconque). Pour \(K\) bits en entrée, on a émis \(N=K/R\) bits codés (cas d’un codage sans poinçonnage).
Fermeture de treillis :
Dans cette méthode, on ajoute aux \(K\) bits d’information \(\nu\) bits (au maximum), dits bits de fermeture (tailing bits), pour rejoindre l’état ‘tout-à-zéro’ du registre (le registre ne contient que des ‘0’). Cela entraîne une baisse du rendement \(R_t\) car pour \(K\) bits d’information, on envoie au plus \((K+\nu)/R_0\), où \(R_0\) et le rendement initial du code. Ici, \(R_t=K/2*(K+2)\). Pour un code récursif, les bits de fermeture dépendent de l’état du registre après \(K\) bits codés et il ne suffit plus de mettre u train de bits \('0'\) pour retourner à l’état ‘tout-à-zéro’ du registre.
Fermeture circulaire de treillis, tail-biting:
Pour ce type de méthode, on réalise un encodage “circulaire” des données ce qui permet de s’affranchir de bits de fermeture et donc d’être plus efficace en rendement. Pour un code convolutif non récursif, ce codage est réalisé en recopiant les \(\nu\) bits de fin de mot d’information au début (sorte de préfixe assurant le caractère cyclique de la convolution entre la séquence d’information et la réponse impulsionelle du filtre associée au codeur). L’état initiale du registre est alors donné par les \(\nu\) bits de fin de mot d’information. On assure ainsi que le codeur terminera dans le même état après \(K\) bits d’information codés. Pour un code récursif, la procédure est un peu plus sophistiquée. Mais l’idée est toujours la même : assurer que le codeur débute et termine le codage dans le même état. Pour \(K\) bits en entrée, on a émis \(N=K/R\) bits codés (cas d’un codage sans poinçonnage).
