3.2. Représentations

On considère de manière générale un codeur avec \(k\) entrées et \(n\) sorties définissant un code convolutif de rendement \(R=k/n\).

3.2.1. Représentation par filtrage

Si on considère le cas simple des codes convolutifs non récursifs, on peut aisément définir chaque sorties comme étant des opérations de filtrage des différentes entrées à l’aide des réponses impulsionnelles finies associées aux fonctions de transfert entre la sorti \(i\) et la sortie \(k\). Ainsi si on note \(\{u^{(1)}[n], u^{(2)}[n], \ldots, u^{(k)}[n]]\}\) les différents flux en entrée du code de rendement \(R=k/n\), on caractérise le transfert entre la sortie \(j\) et l’entrée \(i\) par \(\{g_i^{(j)}[n]\}\). On a alors la sortie \(c^{(j)}[n]\) qui sera donnée par

\[c^{(j)}[n]=\sum_{i=1}^k{g_i^{(j)} \circledast u^{(i)}[n]}.\]

Même si elle s’entend pour les codes récursifs qui ont une réponse impulsionnelle de transfert infinie, cette notation est moins commode que celle qui suit qui utilise la représentation polynomiale.

3.2.2. Représentation vectorielle polynomiale

soient \(\underline{u}(D)=[u^{(1)}(D), u^{(2)}(D), \ldots, u^{(k)}(D)]\), \(\underline{c}(D)=[c^{(1)}(D), c^{(2)}(D), \ldots, c^{(n)}(D)]\), les représentations matricielles des transformées en \(\mathcal{D}\). En prenant la transformée en \(\mathcal{D}\) de \(g_i^{(j)}[n]\) donnée par \(\mathcal{D}\{g_i^{(j)}[n]\}=g_i^{(j)}(D)\), il vient alors

\[\underline{c}(D)=\sum_{i=1}^{k}{u^{(i)}(D)\underline{g}_i(D)}\]

où \(\underline{g}_i(D)=[g_i^{(1)}(D), g_i^{(2)}(D), \ldots g_i^{(n)}(D)]\) et \(g_i^{(j)}(D)\) représente le transfert entre l’entrée \(i\) et la sortie \(j\). On peut alors donner la défintion suivante d’une matrice génératrice polynômiale associée à un code convolutif.

Definition 3.1 (Matrice génératrice polynomiale)

On appelle matrice génératrice polynômiale la matrice \(G(D)\) de taille \(k \times n\) telle que

\[\underline{c}(D)= \underline{u}(D) G(D)\]

avec

\[\begin{split}G(D)=\begin{pmatrix} g_1^{(1)}(D) & g_1^{(2)}(D) & \cdots & g_1^{(n)}(D)\\ g_2^{(1)}(D) & g_2^{(2)}(D) & \cdots & g_2^{(n)}(D)\\ \vdots & \vdots & \cdots & \vdots\\ g_{k-1}^{(1)}(D) & g_{k-1}^{(2)}(D) & \cdots & g_{k-1}^{(n)}(D)\\ g_k^{(1)}(D) & g_k^{(2)}(D) & \cdots & g_k^{(n)}(D)\\ \end{pmatrix}\end{split}\]

Definition 3.2 (Matrice de parité polynomiale)

On peut également pour un code convolutif définir une matrice de parité définie par

\[\underline{c}(D) H^{T}(D)=\bf{0}\]

et donc \(G(D)H^{T}(D)=\bf{0}\)

Ces représentations polynomiales joueront le même rôle que les matrices génératrice et de parité dans le cas de codes en bloc.

3.2.3. Codes convolutifs récursifs

Definition 3.3 (Fonction de transfert récursive)

Certaines relations entrées-sorties peuvent être définies par un transfert de type récursif (ie. à réponse impulsionnelle infinie). Une implémentation simple (Type I) entre l’entrée \(i\) et la sortie \(j\) est donnée par

\[g_i^{(j)}(D)=\frac{b_0 + b_1 D + b_2 D^2 + \ldots+ b_{m} D^m}{1+ a_1 D + a_2 D^2 + \ldots+ a_{m} D^m}\]

dont la représentation sous forme de registre est donnée en figure Fig. 3.2

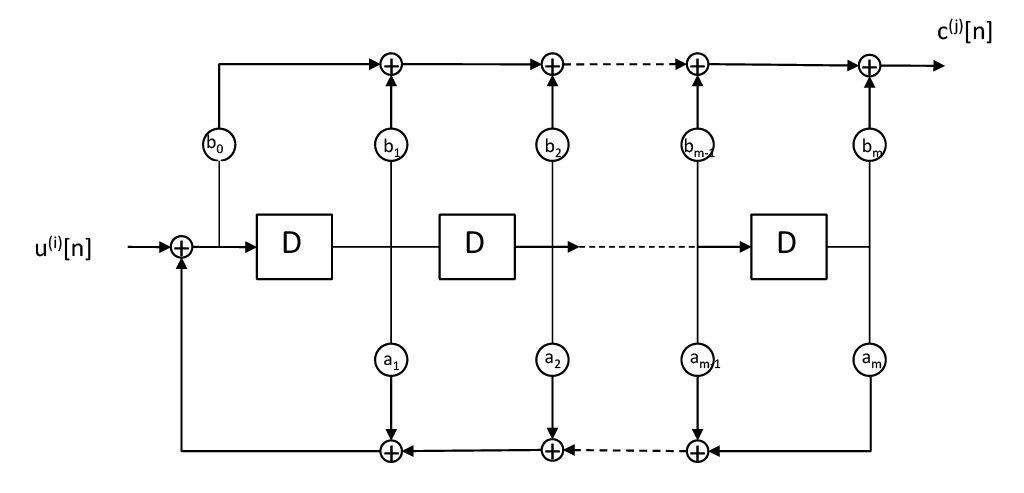
Fig. 3.2 Structure générique d’un transfert récursif.

Dans ce cas, on obtient la relation entrée-sortie suivante

\[c^{(j)}(D)=g_i^{(j)}(D)u^{(i)}(D)\]

ce qui correspond à une écriture plus aisée de l’équation de convolution avec la réponse impulsionnelle infinie donnée par \(c^{(j)}[n]=g_i^{(j)}\circledast u^{(i)}[n]\). Cela correspond en fait à la réalisation à l’aide de l’équation aux différences associées donnée par

\[c^{(j)}[n]=\sum_{l=1}^m{a_l\; c^{(j)}[n-l]}+\sum_{k=0}^m{b_k \;u^{(i)}[n-k]}\]

On retrouve là encore le même formalisme que pour le filtrage en trainement numérique du signal. Un code convolutif défini par une matrice génératrice ayant des éléments de transfert récursifs est appelé code convolutif récursif.

Par exemple, le code récursif systématique \((1,5/7)_8\) a pour matrice génératrice polynomiale

\[G(D)=[1 \frac{1 + D^2}{1+ D + D^2}].\]

Sa représentation est donnée en figure Fig. 3.3

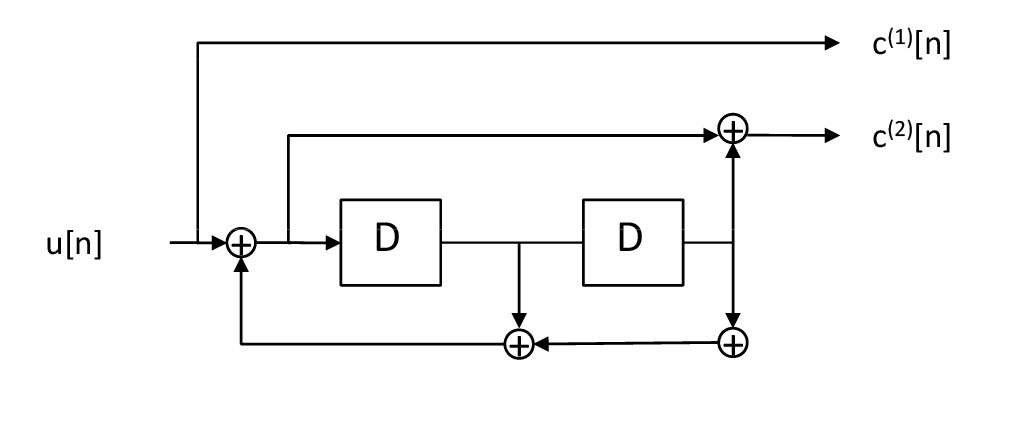
Fig. 3.3 Code récursif \((1,5/7)\).

Example 3.1

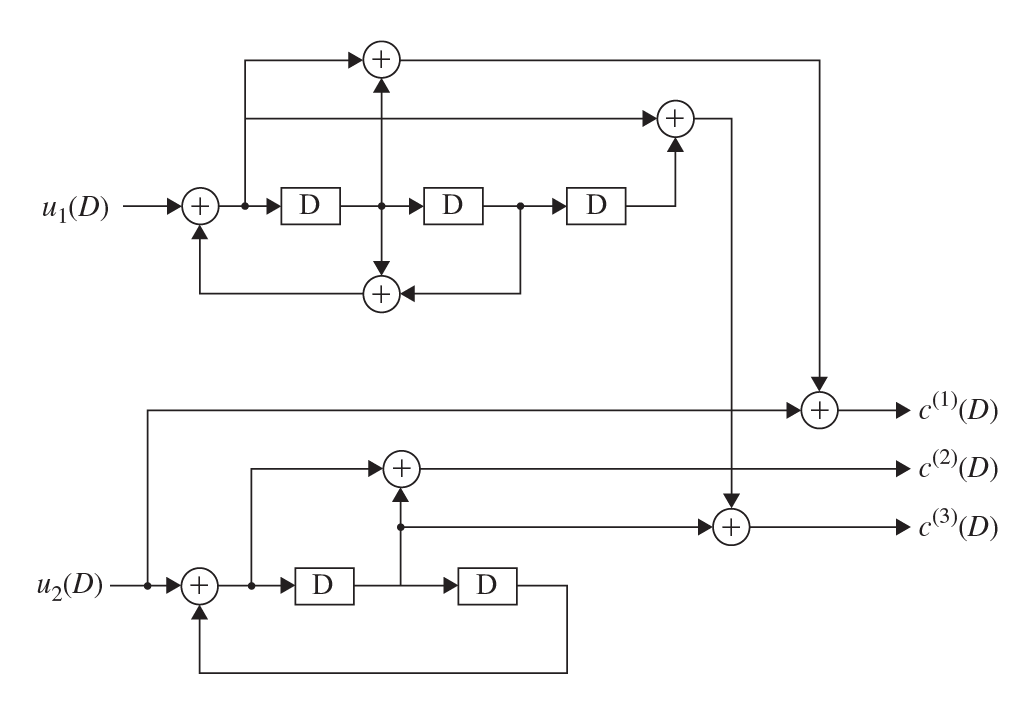
Fig. 3.4 Un exemple de code convolutif de rendement R=2/3.

On considère le code convolutif donné par la figure Fig. 3.4. Montrer que la matrice génératrice polynomiale peut s’écrire comme suit

\[\begin{split}G(D)=\left(\begin{array}{ccc} \frac{1+D}{1+D+D^2}& 0 & {1+D}\\ 1& \frac{1}{1+D} & \frac{D}{1+D^2} \\ \end{array}\right)\end{split}\]

\[\underline{u}(D)=[u_1(D), u_2(D)], \underline{c}(D)=[c_1(D), c_2(D), c_3(D)]\]

3.2.4. Représentation par machine à états finis et diagramme d’état associé.

Sans perte de généralité, on considérera ici un code de rendement \(R=1/n\) pour faciliter l’exposé. Pour un code convolutif, on peut donner une représentation dîte d’état du codeur (automate associé) en définissant un état à partir d’un vecteur représentant le contenu des registres du codeur (la mémoire du codeur). Ainsi si le codeur est dans un état donné \(\underline{S}_n\) (ses registres sont initialisé avec certaines valeurs), la donnée des bits d’entrée permet de donner de manière déterministe les sorties. Ce qui est formellement représenté par le diagramme suivant :

\[\{ u_k \}\rightarrow \fbox{$\underline{S}_k$} \rightarrow \{ c_k \}\]

où \(c_k=[c_k^{(1)}, c_k^{(2)}, c_k^{(n)}]\) et \(\underline{S}_k\) représente l’état interne du registre à décalage.

On peut alors d’écrire ce modèle d’état à l’aide d’équations fonctionnelles

• Equation d’évolution :

Par cette équation, on peut décrire formellement/analytiquement le passage d’un état \(\underline{S}_{k-1}\) à \(\underline{S}_{k}\) en fonction de l’entrée \(u_k\). On écrit cette relation comme

\[\underline{S}_k = F_1(\underline{S}_{k-1},u_k)\]

• Equation d’observation :

Cette équation traduit la génération des sorties observables du modèle et qui sont ici les bits codés \(c_{k}\). On écrit cette relation comme

\[c_k = F_2(\underline{S}_{k-1},u_k)\]

Par exemple, pour le code \((7,5)_8\), on a \(\underline{S}_k=[u_k, u_{k-1}]\). Cette automate peut être visualiser à l’aide d’un diagramme d’état qui est un graphe qui représente les différents états possibles et qui visualise les transitions entre ses états et les sorties associées. Un exemple est donné pour le code convolutif \((7,5)_8\) à la figure Fig. 3.5. Les états représentés par des cercles sont associés au contenu du/des registre(s). Les flèches représentent les transitions entre états et les labels indiquent les bits entrant dans le(s) registre(s) et les bits codés associés.

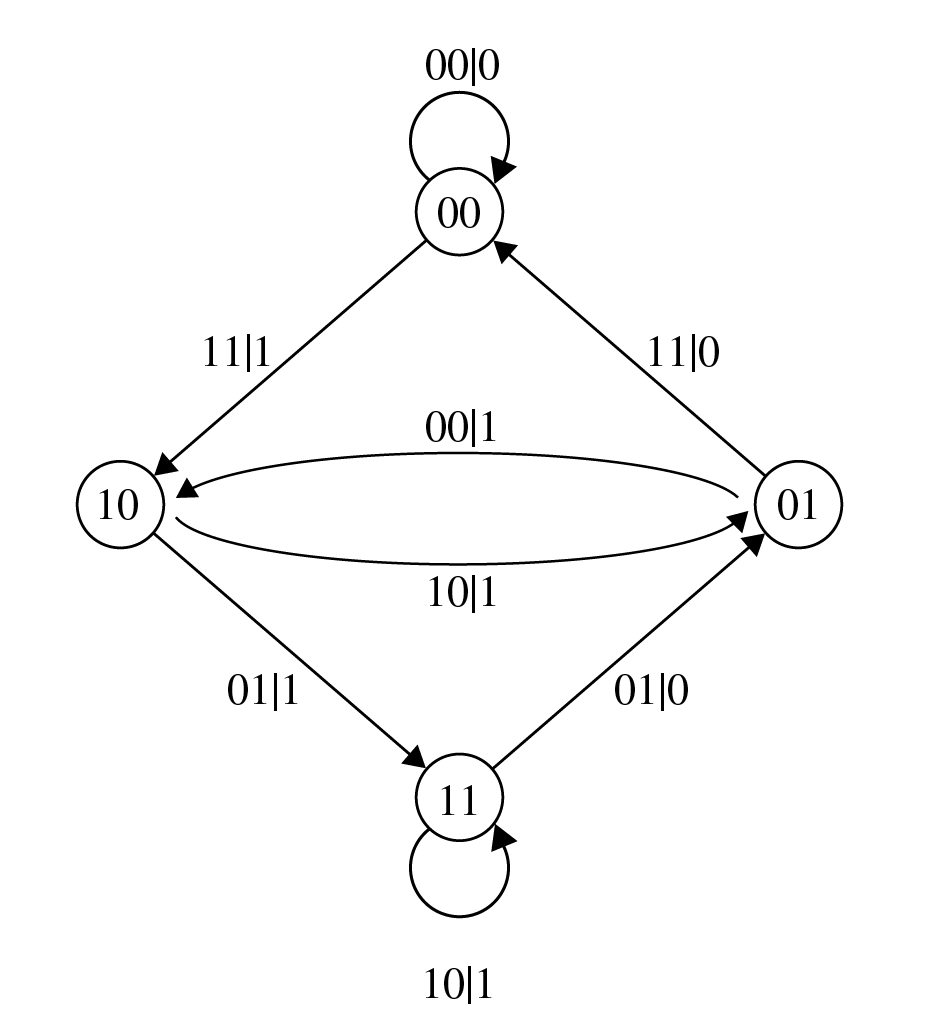
Fig. 3.5 Diagramme d’état du code convolutif \((7,5)_8\).

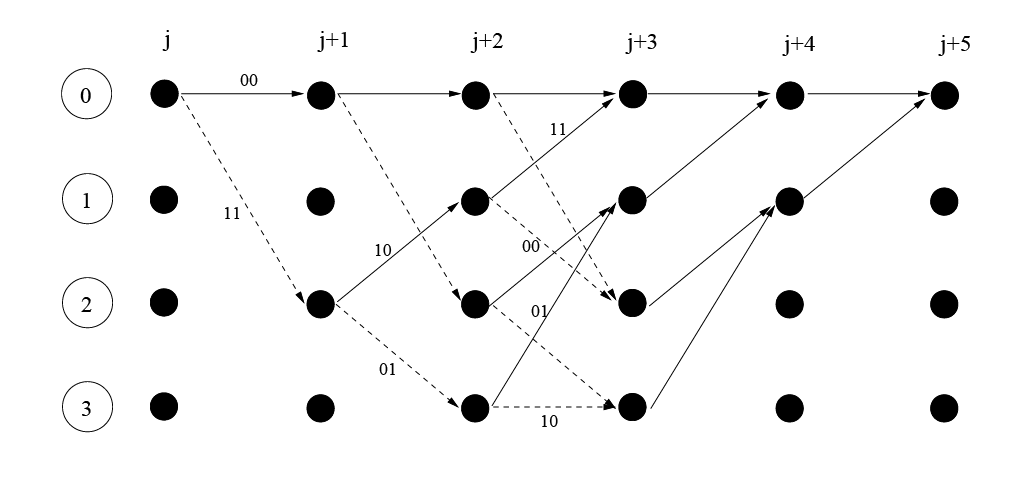
3.2.5. Représentation graphique par un treillis

Definition 3.4 (Treillis d’un code convolutif)

Le treillis est la représentation graphique du code dans son espace d’état en considérant la dimension temporelle. On définit alors les éléments suivants

1. Noeuds : noeuds du graphe associé à un état \(\underline{S}_k\).

2. Transitions : branches entre deux noeuds associées à \(F_1(.)\).

3. Etiquettes/labels : informations portées par les branches (\(u_k,c_k\)) et données par \(F_2(.)\)

Property 3.1

1. Pour un treillis de longueur \(L\), tout chemin du treillis de \(\underline{S}_0\) à \(\underline{S}_L\) est mot de code obtenu par concaténation des étiquettes \(c_k\) du chemin.

2. Le chemin où tous les \(\underline{S}_k\) sont l’état \(\bf{0}\) (représentation binaire naturelle) est le mot de code nul.

3. Événement minimal : chemin qui par de l’état\(\underline{S}_k=\bf{0}\) et ne revient à cet état que à \(\underline{S}_{k+l}\) pour un certain \(l\). On lui associe un poids de Hamming grâce aux étiquettes du chemin.

4. \(d_{\min}\) est donnée par le poids minimal d’un évênement minimal.

Example 3.2 (Code \((7,5)_8\))

Un exemple est donné pour le code \((7,5)_8\) en figure Fig. 3.6

Fig. 3.6 Diagramme d’état du code convolutif \((7,5)_8\).