4.1. Turbo-codes parallèles

On présente ici la concaténation parallèle de codes convolutifs introduite par Claude Berrou en 1993.

4.1.1. Structure du codeur

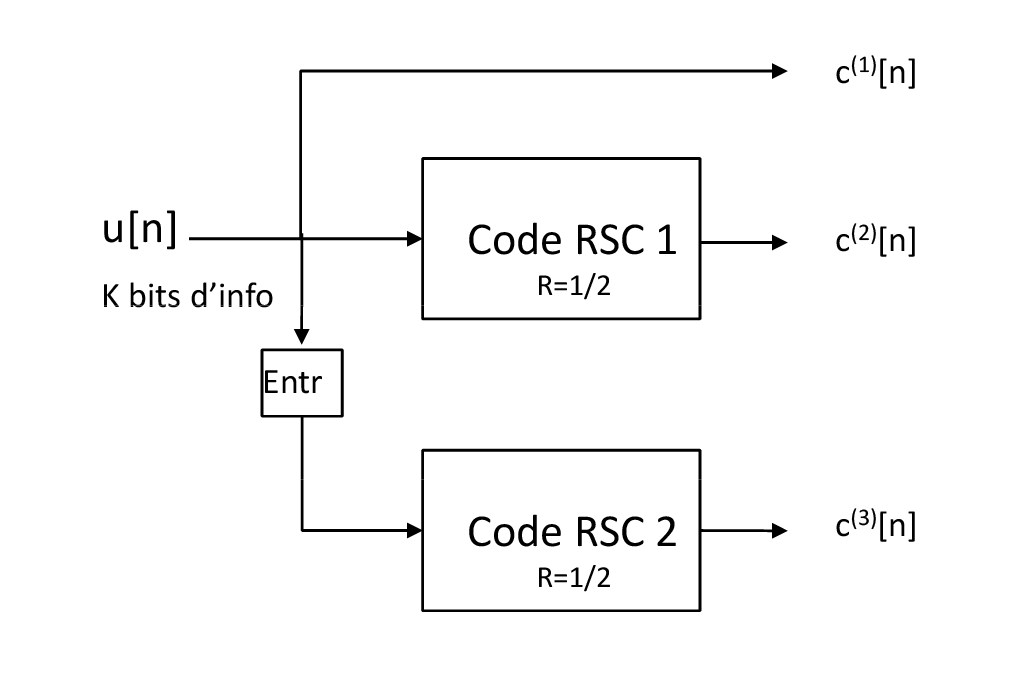
Fig. 4.1 Structure d’un turbo-code parallèle avec deux codeurs.

4.1.1.1. Codage de l’information

La structure d’un turbo-code parallèle avec des codes composants de rendement \(R_0=1/2\) est donnée figure Fig. 4.1. La structure du codeur est une structure de codage par bloc. ELle se généralise à plusieurs codeurs avec des propriétés qui peuvent être différentes. Pour la simplicité d’exposition, on se contentera dans ce texte du cas de deux codeurs identiques ayant les mêmes caractéristiques. La procédure est donnée comme suit

1. \(K\) bits d’information sont codés avec le codeur convolutif récursif systématqiue RSC1,

2. Les mêmes \(K\) bits d’information sont en parallèle entrelacés et codés par le codeur convolutif récursif RSC2,

3. Comme la sortie systèmatique du code RSC1 est déjà disponible, seule la partie redondance est prise en compte sur le codeur RSC2.

En pratique les deux codes sont souvent identiques, cependant rien n’empêche de considérer des codes composants différents et de rendments différents. La seule contrainte originelle est qu’ils partagent la même information. En partant d’un code de rendement \(R_0=1/2\), on obtient donc un code de rendement \(R'_0=1/3\). Le code est par construction systématique. On peut faire varier le rendement en définissant comem pour les codes convolutifs des masques périodiques de poinçonnage. On est donc pas limité au seul rendment \(1/3\). En générale si on considère un code dont les composants sont de rendements \(R_1\) et \(R_2\) le rendement golbale du code est donnée par

\[\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}\]

Ainsi, on peut atteindre différents rendements par changement des codes composants. On peut également employé la technique de poinçonnage comme utilisée avec les codes convolutifs. Par exemple, on peut envoyer, sur deux périodes d’horloge, chaque bit systématique et poinçonnés alternativement chaque bits de parité ce qui donne la matrice de poinçonnage de période \(2\) suivante

\[\begin{split}{\bf P}=\begin{pmatrix} 1 &1 \\ 1 & 0 \\ 0 & 1 \end{pmatrix}\end{split}\]

Le code résultant est un code de rendement \(R=1/2\).

4.1.1.2. Fermeture de treillis

Généralement, un turbo-code est utilisé pour réalisé un codage de type bloc. Dans ce cadre Une terminaison de treillis est souvent réalisée. Cependant la fermeture de treillis ne se réalise pas par un simple ajout de bits \('0'\) pour amener le codeur dans l’état de registre “tout-à-zéro”. Dans le cadre de codes convolutifs récursifs, les \(\nu\) bits à considérer dépendent de l’état du registre près que les \(K\) premiers bits aient été codés. Dans ce cas, la connaissance de cet état permet de déterminer la suite de bits à utiliser. On peut considérer soit une table associée ou de manière plus efficcae de considérer la méthode de Divsalar. Celle-ci consiste en la méthode décrite figure 5.0.1{reference-type=”ref” reference=””}. A près \(K\) bits d’information, l’entrée du codeur est alors rebouclée sur le retour du code récursif qui donne alors la sortie systématique et à pour effet de conduire le codeur à l’état “tout-à-zéro”. La présence de l’entrelaceur prévient toute fermeture conjointe des deux codeurs avec un nombre de bits raisonnable pour un entrelaceur quelconque. Ainsi, on ne considère donc en générale que la fermeture du premier code composant, le second n’étant pas terminé. On verra par la suite comment gérer dans le décodage cette asymmétrie.

4.1.1.3. Entrelaceur

Théoriquement L’entrelaceur utilisée dans le codage de type turbo est un entrelaceur en bloc pseudo-aléatoire défini comme une permutation de \(K\) éléments (les \(K\) bits d’information) sans répétition. Un des rôles principaux est de pouvoir décorréler les entrées souples des décodeurs souples associés. Nous verrons par la suite comment sont réalisés ces entrelaceurs.

4.1.2. Décodage itératif des turbo-codes

Du schéma du codeur, on voit clairement que l’on peut décoder les deux codes constituants de manière indépendantes car on a accès pour les deux codes aux bits systématiques et codés. Cependant, cette stratégie est sous optimale car les bits d’information traités par les deux codeurs ne sont pas indépendants. En effet, les deux codeurs partagent la même information et on peut alors se poser la question d’un décodage conjoint des deux codes convolutifs. Le fait d’avoir un entrelaceur implique une complexité exponentielle du décodage conjoint si l’on voulait considérer un treillis conjoint. L’idée proposée par C. Berrou est de décoder séparément les deux codes constituants. Chaque codeur pourra être à même de renseigner l’autre codeur d’une probabilité a priori pour les bits d’information qu’ils ont en commun, a priori qui pourra alors être mis à profis pour une nouvelle tentative de décodage. On peut alors envisager une sorte de décodage successif collaboratif des deux décodeurs. La difficulté est d’assurer que l’information échangée est suffisament décoréllée entre les deux décodeurs. Pour cela nous avons besoin de définir une quantité appelée information extinsèque qui est une quantité qui est liée au gain statistique apporté par le décodeur sur le décodage souple d’un bit hormis la vraisemblance et l’a priori disponible.

4.1.2.1. Notion d’Information Extrinsèque

On se contentera ici du cas d’un codeur récursif systématique de rendement \(R=1/n_c\), pour simplifier les notations. On supposera également que \(c^{(1)}_n=u_n\), ie. le premier bit codé par le codeur RSC1 est le bit systématique. On peut alors à partir du décodage MAP symbole mettre en exergue l’information dîte extinsèque:

Definition 4.1 (Information extrinsèque)

Pour un codeur RSC, le LLR associé à un décodage de type MAP peut être décomposé de la manière suivante:

\[\begin{split}\begin{aligned} \textstyle L(u_n)&\textstyle =&\textstyle \log{\left[\frac{ \sum_{\mathcal{S}^{+}}{p(s_{n-1}=s', s_{n}=s, { \bf y})}}{\sum_{\mathcal{S}^{-}}{p(s_{n-1}=s', s_{n}=s, { \bf y})}}\right]} \\ \textstyle & \textstyle =& \textstyle {\bf L_c(u_n)} + {\bf L_{a}(u_n)} + {\bf L_{ext}(u_n)} \end{aligned}\end{split}\]

avec

1. Information canal (Vraisemblance) :

   \[L_c(u_n) = \log{(\frac{p(y^{(1)}_n|u_n=+1)}{p(y^{(1)}_n|u_n=-1)})}\]

2. Information a priori :

   \[L_{a}(u_n) = \log{(\frac{p(u_n=+1)}{p(u_n=-1)})}\]

3. Information extrinsèque : $\(\begin{aligned} \textstyle L_{ext}(u_n)&\textstyle =& \textstyle \log{\left[\frac{ \sum_{\mathcal{S}^{+}}{\alpha_{n-1}(s') \prod_{k=2}^{n_c}{p(y^{(k)}_n|c^{(k)}_n(s',s))} \beta_{n}(s)}}{\sum_{\mathcal{S}^{-}}{\alpha_{n-1}(s') \prod_{l=2}^{n_c}{p(y^{(l)}_n|c^{(l)}_n(s',s))} \beta_{n}(s)}}\right]} \nonumber \\ \textstyle & \textstyle =& \textstyle \log{\left[\frac{ \sum_{\mathcal{S}^{+}}{\alpha_{n-1}(s') \gamma_n^{e}(s',s) \beta_{n}(s)}}{\sum_{\mathcal{S}^{-}}{\alpha_{n-1}(s') \gamma_n^{e}(s',s) \beta_{n}(s)}}\right]} \end{aligned}\)$

On peut alors faire l’interprétation suivante. En non codée, nous aurions

\[\begin{split}\begin{aligned} L(u_n)&=& {\bf L_c(u_n)} + {\bf L_{a}(u_n)} \nonumber \\ &=& \log{(\frac{p(y^{(1)}_n|u_n=+1)}{p(y^{(1)}_n|u_n=-1)})} + \log{(\frac{p(u_n=+1)}{p(u_n=-1)})}. \end{aligned}\end{split}\]

Ce qui correspond à la statistique de test classique de la détection d’une variable binaire en fonction de sa vraisemblance et de l’a priori disponible. Pour le cas codé, la quantité \(L_{ext}(u_n)\) représente un terme supplémentaire, qui est lié au code et au processus de décodage. Elle est extrinsèque car ne dépend pas de l’observations directe du bit ni de son apriori, mais de toutes les autres données. C’est cette quantité qui après décodage MAP par l’agorithme BCJR permet d’avoir un gain par rapport au cas non codé. C’est cette quantité qui sera utilisé à la sortie d’un des deux décodeurs comme a priori pour l’autre décodeur.

Le décodage MAP d’un code convolutif peut donc se représenter par un bloc de décodage à entrées et sorties souples (bloc SISO). Le schéma bloc est donné ci-après.

4.1.2.2. Décodage itératif MAP

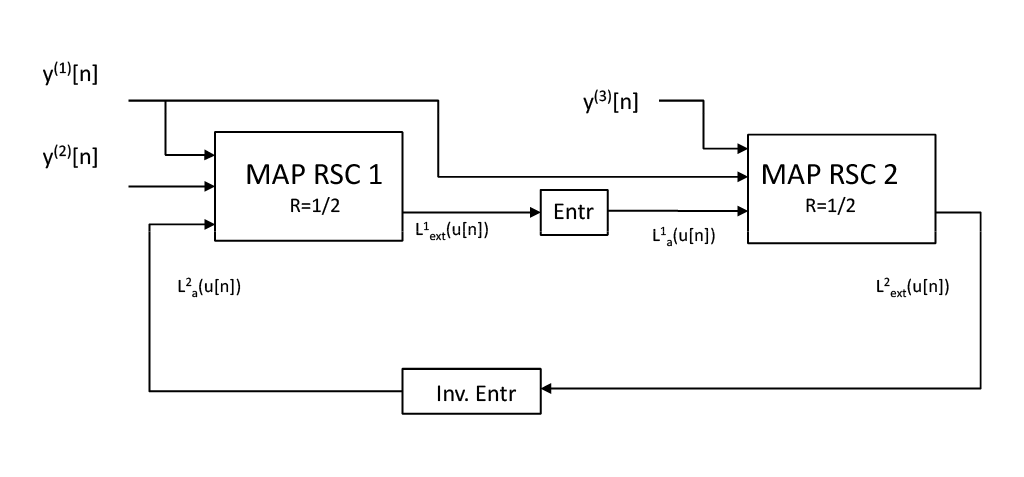
Fig. 4.2 Structure du décodeur itératif pour la concaténation parallèle

Le schéma en figure Fig. 4.2 donne la structure du décodeur itératif turbo. Le principe sous-jacent est le décodage distribué des deux codes composants qui vont avoir un décodage alterné. Les décodeurs MAP des deux codes constituants vont alors pouvoir s’échanger une information extrinsèque relative aux bits d’information communs de manière itérative. L’information extrinsèque sur chaque bit en sortie de chaque codeur est alors considérée par l’autre décodeur comme un a priori après entrelacement/désentrelacement, l’entrelacement favorisant la décorrélation de ces quantités. Le décodage s’effectue comme suit. Un premier décodage MAP est effectué sur le premier code RSC1 pour lequel on ne considère pas d’apriori (ie. \(L_{a,0}(u[n])=0, \forall n\)). L’information extrinsèque du premier codeur est alors calculée comme

\[L_{\mathrm{ext},1}^1(u[n])=L_{1}^1(u[n])-L_c(u[n])-L_{a,0}^1(u[n])\]

Le décodage MAP complet est alors donné par la procédure générique suivante:

• Critères MAP au deux décodeurs à l’itération \((\ell)\):

  \[\begin{split}\begin{aligned} L_{\tiny RSC_1}^{(\ell)}(u_n)&=&\frac{2}{\sigma^2} y_n^{(1)} + L_{a,1}^{(\ell - 1)}(u_n) + L_{e,1}^{(\ell)}(u_n) \nonumber \\ &=&\frac{2}{\sigma^2} y_n^{(1)} + L_{e,2}^{(\ell -1)}(u_{\pi^{-1}(n)}) + L_{e,1}^{(\ell)}(u_n) \end{aligned}\end{split}\]
  \[\begin{split}\begin{aligned} L_{\tiny RSC_2}^{(\ell)}(u_{\pi(n)})&=&\frac{2}{\sigma^2} \pi(y_{\pi(n)}^{(1)}) + L_{e,1}^{(\ell -1)}(u_{\pi(n)}) + L_{e,2}^{(\ell)}(u_{\pi(n)}) \nonumber \\ \end{aligned}\end{split}\]

  avec \(\pi(.)\) et \(\pi^{-1}\) représentent les opérations d’entrelacement et de désentrelacement