Filtrage de Wiener

5.3. Filtrage de Wiener#

5.3.1. Définition#

Le filtre de Wiener est un filtre qui permet de débruiter un signal aléatoire stationnaire de densité spectrale de puissance connue noyé dans un bruit additif supposé également stationnaire. On considère donc deux processus aléatoires stationnaires $I(t)$ et $B(t)$ de moyennes nulles (ce qui simplifie un peu l’analyse) $E[B(t)]=E[I(t)]=0$, de fonctions d’autocorrélation $R_I(\tau), R_B(\tau)$ et de densités spectrales de puissance $s_I(f)$ et $s_B(f)$. On suppose qu’on peut observer

\[ X(t)=I(t)+B(t), \quad t \in \Delta \subset \mathbb{R} \]

et on cherche la meilleure estimation de $I(t)$ notée $\widehat{I}(t)$ obtenue par filtrage linéaire de $X(t)$.

5.3.2. Expression du filtre#

D’après le principe de la projection orthogonale illustré sur la figure ci-dessous,

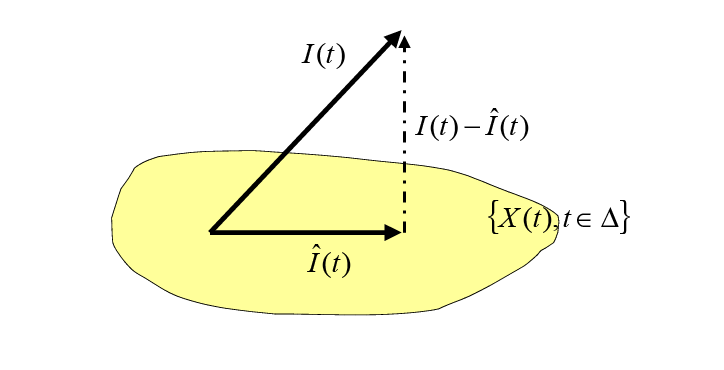
la solution de ce problème vérifie les équations normales définies par

\[ E\left\{ \left[I(t)- \widehat{I}(t) \right] X^{\ast}(u)\right\}=0 \quad \forall u \]

ou

\[ E\left[I(t) I^{\ast}(u)\right] = E\left[\widehat{I}(t) X^{\ast}(u)\right] \quad \forall u \label{normal} \]

En remarquant que $E\left[I(t) I^{\ast}(u)\right] =R_I(t-u)$ et que $\widehat{I}(t)=X(t)*h(t)=\int X(v) h(t-v)dv$, où $h(t)$ est la réponse impulsionnelle recherchée, on obtient

\[ E\left\{ \left[ \widehat{I}(t) X^{\ast} (u)\right]\right\} = \int h(t-v) R_X(v-u)dv = \int h(x) R_X(t-u-x)dx. \]

Les équations normales permettent alors d’obtenir

\[ R_I(y)=\int h(x) R_X(y-x)dx = h(y) \ast R_X(y) \quad \forall y. \]

On en déduit l’expression de la transmittance du filtre recherché $H(f)$ en fonction des densités spectrales de puissance de $I(t)$ et de $B(t)$

\[ H(f)=\frac{s_I(f)}{s_X(f)} = \frac{s_I(f)}{s_I(f)+s_B(f)} \]

5.3.3. Expression du filtre#

L’erreur d’estimation entre $I(t)$ et $ \widehat{I}(t)$ possède une expression très simple qui est définie par

\[ \sigma^2=E\left[ |I(t)- \widehat{I}(t) |^2 \right] = \int \frac{s_I(f) s_B(f)}{s_I(f)+s_B(f)} df \]

En effet

\[ \begin{eqnarray*} \sigma^2 &=& E\left[ |I(t)- \widehat{I}(t) |^2 \right] \cr &=& E\left\{ \left[I(t)- \widehat{I}(t)\right] I^{\ast}(t) \right\} \quad \text{(car $I(t)- \widehat{I}(t)$ est orthogonal à $ \widehat{I}(t)$)} \cr &=& R_I(0)-E\left[\widehat{I}(t) I^{\ast}(t) \right] \end{eqnarray*} \]

Le second terme de cette égalité peut se calculer simplement comme suit, en utilisant $\widehat{I}(t)=X(t)*h(t)=\int X(u) h(t-u)dv$ et $X(u)=I(u)+B(u)$

\[ \begin{eqnarray*} E\left[\widehat{I}(t) I^{\ast}(t) \right] &=& \int h(t-u) E\left[ I(u) I^{\ast}(t) \right] du + \int h(t-u) E\left[ B(u) I^{\ast}(t) \right] \cr &=& \int h(x) R_I^{\ast}(x)dx \end{eqnarray*} \]

d’où

\[ \begin{eqnarray*} \sigma^2 = \int s_I(f)df - \int H(f) s_I(f)df = \int \frac{s_I(f) s_B(f)}{s_I(f)+s_B(f)} df \end{eqnarray*} \]

On peut faire les remarques suivantes :

l’erreur est nulle lorsqu’il n’y a pas de bruit (i.e., lorsque $s_b(f)=0$)
l’erreur est nulle lorsque les DSP du signal et du bruit ont des supports disjoints (ce qui implique $s_I(f)s_B(f)=0$)

5.3.4. Applications#

Une application classique du filtre de Wiener est le débruitage d’images. Quelques résultats obtenus avec cette méthode sont présentés dans les images ci-dessous. Pour plus de détails concernant le filtre de Wiener, le lecteur pourra consulter l’ouvrage de Zaknich [Zaknich, 2005].